Photoelectric effect

Light–matter interaction
Low-energy phenomena:
Photoelectric effect
Mid-energy phenomena:
Compton scattering
High-energy phenomena:
Pair production

In the photoelectric effect, electrons are emitted from matter (metals and non-metallic solids, liquids or gases) as a consequence of their absorption of energy from electromagnetic radiation of very short wavelength, such as visible or ultraviolet light. Electrons emitted in this manner may be referred to as photoelectrons.[1][2] First observed by Heinrich Hertz in 1887,[2][3] the phenomenon is also known as the Hertz effect,[4][5] although the latter term has fallen out of general use. Hertz observed and then showed that electrodes illuminated with ultraviolet light create electric sparks more easily.

The photoelectric effect requires photons with energies from a few electronvolts to over 1 MeV in high atomic number elements. Study of the photoelectric effect led to important steps in understanding the quantum nature of light and electrons and influenced the formation of the concept of wave–particle duality.[1] Other phenomena where light affects the movement of electric charges include the photoconductive effect (also known as photoconductivity or photoresistivity), the photovoltaic effect, and the photoelectrochemical effect.

Contents

Emission mechanism

The photons of a light beam have a characteristic energy proportional to the frequency of the light. In the photoemission process, if an electron within some material absorbs the energy of one photon and acquires more energy than the work function (the electron binding energy) of the material, it is ejected. If the photon energy is too low, the electron is unable to escape the material. Increasing the intensity of the light beam increases the number of photons in the light beam, and thus increases the number of electrons excited, but does not increase the energy that each electron possesses. The energy of the emitted electrons does not depend on the intensity of the incoming light, but only on the energy or frequency of the individual photons. It is an interaction between the incident photon and the outermost electron.

Electrons can absorb energy from photons when irradiated, but they usually follow an "all or nothing" principle. All of the energy from one photon must be absorbed and used to liberate one electron from atomic binding, or else the energy is re-emitted. If the photon energy is absorbed, some of the energy liberates the electron from the atom, and the rest contributes to the electron's kinetic energy as a free particle.[6][7][8]

Experimental results of the photoelectric emission

  1. For a given metal and frequency of incident radiation, the rate at which photoelectrons are ejected is directly proportional to the intensity of the incident light.
  2. For a given metal, there exists a certain minimum frequency of incident radiation below which no photoelectrons can be emitted. This frequency is called the threshold frequency.
  3. For a given metal of particular work function, increase in intensity of incident beam increases the magnitude of the photoelectric current, though stopping voltage remains the same.
  4. For a given metal of particular work function, increase in frequency of incident beam increases the maximum kinetic energy with which the photoelectrons are emitted. Thus the stopping voltage increases. In practice the number of electrons does change because the probability that each photon results in an emitted electron is a function of photon energy.
  5. Above the threshold frequency, the maximum kinetic energy of the emitted photoelectron depends on the frequency of the incident light, but is independent of the intensity of the incident light so long as the latter is not too high [9]
  6. The time lag between the incidence of radiation and the emission of a photoelectron is very small, less than 10−9 second.
  7. The direction of distribution of emitted electrons peaks in the direction of polarization (the direction of the electric field) of the incident light, if it is linearly polarized.[10]

Mathematical description

The maximum kinetic energy 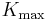K_{\mathrm{max}} of an ejected electron is given by

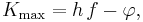
K_{\mathrm{max}} = h\,f - \varphi,

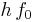where h is the Planck constant and f is the frequency of the incident photon. The term φ = h\,f_0 is the work function (sometimes denoted W), which gives the minimum energy required to remove a delocalised electron from the surface of the metal. The work function satisfies

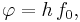
\varphi = h\,f_0,

where 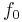f_0 is the threshold frequency for the metal. The maximum kinetic energy of an ejected electron is then

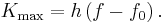
K_{\mathrm{max}} = h \left(f - f_0\right).

Kinetic energy is positive, so we must have 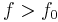f > f_0 for the photoelectric effect to occur.[11]

Stopping potential

The relation between current and applied voltage illustrates the nature of the photoelectric effect. For discussion, a light source illuminates a plate P, and another plate electrode Q collects any emitted electrons. We vary the potential between P and Q and measure the current flowing in the external circuit between the two plates.

If the frequency and the intensity of the incident radiation are fixed, the photoelectric current increases gradually with an increase in positive potential until all the photoelectrons emitted are collected. The photoelectric current attains a saturation value and does not increase further for any increase in the positive potential. The saturation current depends on the intensity of illumination, but not its wavelength.

If we apply a negative potential to plate Q with respect to plate P and gradually increase it, the photoelectric current decreases until it is zero, at a certain negative potential on plate Q. The minimum negative potential given to plate Q at which the photoelectric current becomes zero is called stopping potential or cut off potential.[12]

i. For the given frequency of incident radiation, the stopping potential is independent of its intensity.

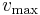ii. For a given frequency of the incident radiation, the stopping potential Vo is related to the maximum kinetic energy of the photoelectron that is just stopped from reaching plate Q. If m is the mass and v_{\mathrm{max}} is the maximum velocity of photoelectron emitted, then

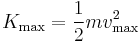
K_{\mathrm{max}} = \frac {1} {2} m v^2_{\mathrm{max}}

If e is the charge on the electron and 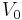V_0 is the stopping potential, then the work done by the retarding potential in stopping the electron 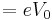= eV_0, which gives

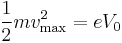
{1\over 2}mv^2_{\mathrm{max}} = eV_0

The above relation shows that the maximum velocity of the emitted photoelectron is independent of the intensity of the incident light. Hence,

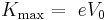
K_{\mathrm{max}} =\ eV_0

The stopping voltage varies linearly with frequency of light, but depends on the type of material. For any particular material, there is a threshold frequency that must be exceeded, independent of light intensity, to observe any electron emission.

Three-step model

In the X-ray regime, the photoelectric effect in crystalline material is often decomposed into three steps:[13]

  1. Inner photoelectric effect (see photodiode below). The hole left behind can give rise to auger effect, which is visible even when the electron does not leave the material. In molecular solids phonons are excited in this step and may be visible as lines in the final electron energy. The inner photoeffect has to be dipole allowed. The transition rules for atoms translate via the tight-binding model onto the crystal. They are similar in geometry to plasma oscillations in that they have to be transversal.
  2. Ballistic transport of half of the electrons to the surface. Some electrons are scattered.
  3. Electrons escape from the material at the surface.

In the three-step model, an electron can take multiple paths through these three steps. All paths can interfere in the sense of the path integral formulation. For surface states and molecules the three-step model does still make some sense as even most atoms have multiple electrons which can scatter the one electron leaving.

History

When a surface is exposed to electromagnetic radiation above a certain threshold frequency (typically visible light for alkali metals, near ultraviolet for other metals, and extreme ultraviolet for non-metals), the radiation is absorbed and electrons are emitted. Light, and especially ultra-violet light, discharges negatively electrified bodies with the production of rays of the same nature as cathode rays.[14] Under certain circumstances it can directly ionize gases.[14] The first of these phenomena was discovered by Hertz and Hallwachs in 1887.[14] The second was announced first by Philipp Lenard in 1900.[14]

The ultra-violet light to produce these effects may be obtained from an arc lamp, or by burning magnesium, or by sparking with an induction coil between zinc or cadmium terminals, the light from which is very rich in ultra-violet rays. Sunlight is not rich in ultra-violet rays, as these have been absorbed by the atmosphere, and it does not produce nearly so large an effect as the arc-light. Many substances besides metals discharge negative electricity under the action of ultraviolet light: lists of these substances will be found in papers by G. C. Schmidt[15] and O. Knoblauch.[16]

19th century

In 1839, Alexandre Edmond Becquerel discovered the photovoltaic effect while studying the effect of light on electrolytic cells.[17] Though not equivalent to the photoelectric effect, his work on photovoltaics was instrumental in showing a strong relationship between light and electronic properties of materials. In 1873, Willoughby Smith discovered photoconductivity in selenium while testing the metal for its high resistance properties in conjunction with his work involving submarine telegraph cables.[18]

Johann Elster (1854–1920) and Hans Geitel (1855–1923), students in Heidelberg, developed the first practical photoelectric cells that could be used to measure the intensity of light.[19] Elster and Geitel had investigated with great success the effects produced by light on electrified bodies.[20]

In 1887, Heinrich Hertz observed the photoelectric effect and the production and reception of electromagnetic waves.[14] He published these observations in the journal Annalen der Physik. His receiver consisted of a coil with a spark gap, where a spark would be seen upon detection of electromagnetic waves. He placed the apparatus in a darkened box to see the spark better. However, he noticed that the maximum spark length was reduced when in the box. A glass panel placed between the source of electromagnetic waves and the receiver absorbed ultraviolet radiation that assisted the electrons in jumping across the gap. When removed, the spark length would increase. He observed no decrease in spark length when he substituted quartz for glass, as quartz does not absorb UV radiation. Hertz concluded his months of investigation and reported the results obtained. He did not further pursue investigation of this effect.

The discovery by Hertz[21] in 1887 that the incidence of ultra-violet light on a spark gap facilitated the passage of the spark, led immediately to a series of investigations by Hallwachs,[22] Hoor,[23] Righi[24] and Stoletow.[25][26][27][28][29][30][31] on the effect of light, and especially of ultra-violet light, on charged bodies. It was proved by these investigations that a newly cleaned surface of zinc, if charged with negative electricity, rapidly loses this charge however small it may be when ultra-violet light falls upon the surface; while if the surface is uncharged to begin with, it acquires a positive charge when exposed to the light, the negative electrification going out into the gas by which the metal is surrounded; this positive electrification can be much increased by directing a strong airblast against the surface. If however the zinc surface is positively electrified it suffers no loss of charge when exposed to the light: this result has been questioned, but a very careful examination of the phenomenon by Elster and Geitel[32] has shown that the loss observed under certain circumstances is due to the discharge by the light reflected from the zinc surface of negative electrification on neighbouring conductors induced by the positive charge, the negative electricity under the influence of the electric field moving up to the positively electrified surface.[33]

With regard to the Hertz effect, the researches from the start showed a great complexity of the phenomenon of photoelectric fatigue — that is, the progressive diminution of the effect observed upon fresh metallic surfaces. According to an important research by Wilhelm Hallwachs, ozone played an important part in the phenomenon.[34] However, other elements enter such as oxidation, the humidity, the mode of polish of the surface, etc. It was at the time not even sure that the fatigue is absent in a vacuum.

In the period from February 1888 and until 1891, a detailed analysis of photoeffect was performed by Aleksandr Stoletov with results published in 6 works; four of them in Comptes Rendus, one review in Physikalische Revue (translated from Russian), and the last work in Journal de Physique. First, in these works Stoletov invented a new experimental setup which was more suitable for a quantitative analysis of photoeffect. Using this setup, he discovered the direct proportionality between the intensity of light and the induced photo electric current (the first law of photoeffect or Stoletov's law). One of his other findings resulted from measurements of the dependence of the intensity of the electric photo current on the gas pressure, where he found the existence of an optimal gas pressure Pm corresponding to a maximum photocurrent; this property was used for a creation of solar cells.

In 1899, J. J. Thomson investigated ultraviolet light in Crookes tubes.[35] Influenced by the work of James Clerk Maxwell, Thomson deduced that cathode rays consisted of negatively charged particles, later called electrons, which he called "corpuscles". In the research, Thomson enclosed a metal plate (a cathode) in a vacuum tube, and exposed it to high frequency radiation. It was thought that the oscillating electromagnetic fields caused the atoms' field to resonate and, after reaching a certain amplitude, caused a subatomic "corpuscle" to be emitted, and current to be detected. The amount of this current varied with the intensity and colour of the radiation. Larger radiation intensity or frequency would produce more current.

20th century

The discovery of the ionization of gases by ultra-violet light was made by Philipp Lenard in 1900. As the effect was produced across several centimeters of air and made very great positive and small negative ions, it was natural to interpret the phenomenon, as did J. J. Thomson, as a Hertz effect upon the solid or liquid particles present in the gas.[14]

In 1902, Lenard observed that the energy of individual emitted electrons increased with the frequency (which is related to the color) of the light.[6]

This appeared to be at odds with James Clerk Maxwell's wave theory of light, which was thought to predict that the electron energy would be proportional to the intensity of the radiation.

Lenard observed the variation in electron energy with light frequency using a powerful electric arc lamp which enabled him to investigate large changes in intensity, and that had sufficient power to enable him to investigate the variation of potential with light frequency. His experiment directly measured potentials, not electron kinetic energy: he found the electron energy by relating it to the maximum stopping potential (voltage) in a phototube. He found that the calculated maximum electron kinetic energy is determined by the frequency of the light. For example, an increase in frequency results in an increase in the maximum kinetic energy calculated for an electron upon liberation – ultraviolet radiation would require a higher applied stopping potential to stop current in a phototube than blue light. However Lenard's results were qualitative rather than quantitative because of the difficulty in performing the experiments: the experiments needed to be done on freshly cut metal so that the pure metal was observed, but it oxidised in a matter of minutes even in the partial vacuums he used. The current emitted by the surface was determined by the light's intensity, or brightness: doubling the intensity of the light doubled the number of electrons emitted from the surface.

The researches of Langevin and those of Eugene Bloch[36] have shown that the greater part of the Lenard effect is certainly due to this 'Hertz effect'. The Lenard effect upon the gas itself nevertheless does exist. Refound by J. J. Thomson[37] and then more decisively by Frederic Palmer, Jr.,[38][39] it was studied and showed very different characteristics than those at first attributed to it by Lenard.[14]

In 1905, Albert Einstein solved this apparent paradox by describing light as composed of discrete quanta, now called photons, rather than continuous waves. Based upon Max Planck's theory of black-body radiation, Einstein theorized that the energy in each quantum of light was equal to the frequency multiplied by a constant, later called Planck's constant. A photon above a threshold frequency has the required energy to eject a single electron, creating the observed effect. This discovery led to the quantum revolution in physics and earned Einstein the Nobel Prize in Physics in 1921.[40] By wave-particle duality the effect can be analyzed purely in terms of waves though not as conveniently.[41]

Albert Einstein's mathematical description of how the photoelectric effect was caused by absorption of quanta of light (now called photons), was in one of his 1905 papers, named "On a Heuristic Viewpoint Concerning the Production and Transformation of Light". This paper proposed the simple description of "light quanta", or photons, and showed how they explained such phenomena as the photoelectric effect. His simple explanation in terms of absorption of discrete quanta of light explained the features of the phenomenon and the characteristic frequency. Einstein's explanation of the photoelectric effect won him the Nobel Prize in Physics in 1921.[42]

The idea of light quanta began with Max Planck's published law of black-body radiation ("On the Law of Distribution of Energy in the Normal Spectrum"[43]) by assuming that Hertzian oscillators could only exist at energies E proportional to the frequency f of the oscillator by E = hf, where h is Planck's constant. By assuming that light actually consisted of discrete energy packets, Einstein wrote an equation for the photoelectric effect that agreed with experimental results. It explained why the energy of photoelectrons were dependent only on the frequency of the incident light and not on its intensity: a low-intensity, high-frequency source could supply a few high energy photons, whereas a high-intensity, low-frequency source would supply no photons of sufficient individual energy to dislodge any electrons. This was an enormous theoretical leap, but the concept was strongly resisted at first because it contradicted the wave theory of light that followed naturally from James Clerk Maxwell's equations for electromagnetic behavior, and more generally, the assumption of infinite divisibility of energy in physical systems. Even after experiments showed that Einstein's equations for the photoelectric effect were accurate, resistance to the idea of photons continued, since it appeared to contradict Maxwell's equations, which were well-understood and verified.

Einstein's work predicted that the energy of individual ejected electrons increases linearly with the frequency of the light. Perhaps surprisingly, the precise relationship had not at that time been tested. By 1905 it was known that the energy of photoelectrons increases with increasing frequency of incident light and is independent of the intensity of the light. However, the manner of the increase was not experimentally determined until 1914 when Robert Andrews Millikan showed that Einstein's prediction was correct.[7]

The photoelectric effect helped propel the then-emerging concept of the dualistic nature of light, that light simultaneously possesses the characteristics of both waves and particles, each being manifested according to the circumstances. The effect was impossible to understand in terms of the classical wave description of light,[44][45][46] as the energy of the emitted electrons did not depend on the intensity of the incident radiation. Classical theory predicted that the electrons would 'gather up' energy over a period of time, and then be emitted.[45][47]

Uses and effects

Photomultipliers

Main article: Photomultiplier

These are extremely light-sensitive vacuum tubes with a photocathode coated onto part (an end or side) of the inside of the envelope. The photocathode contains combinations of materials such as caesium, rubidium and antimony specially selected to provide a low work function, so when illuminated even by very low levels of light, the photocathode readily releases electrons. By means of a series of electrodes (dynodes) at ever-higher potentials, these electrons are accelerated and substantially increased in number through secondary emission to provide a readily detectable output current. Photomultipliers are still commonly used wherever low levels of light must be detected.[48]

Image sensors

Video camera tubes in the early days of television used the photoelectric effect, for example, Philo Farnsworth's "Image dissector" used a screen charged by the photoelectric effect to transform an optical image into a scanned electronic signal.[49]

Gold-leaf electroscope

Gold-leaf electroscopes are designed to detect static electricity. Charge placed on the metal cap spreads to the stem and the gold leaf of the electroscope. Because they then have the same charge, the stem and leaf repel each other. This will cause the leaf to bend away from the stem. The electroscope is an important tool in illustrating the photoelectric effect. For example, if the electroscope is negatively charged throughout, there is an excess of electrons and the leaf is separated from the stem. If high-frequency light shines on the cap, the electroscope discharges and the leaf will fall limp. This is because the frequency of the light shining on the cap is above the cap's threshold frequency. The photons in the light have enough energy to liberate electrons from the cap, reducing its negative charge. This will discharge a negatively charged electroscope and further charge a positive electroscope. However, if the electromagnetic radiation hitting the metal cap does not have a high enough frequency (its frequency is below the threshold value for the cap), then the leaf will never discharge, no matter how long one shines the low-frequency light at the cap.[50]

Photoelectron spectroscopy

Since the energy of the photoelectrons emitted is exactly the energy of the incident photon minus the material's work function or binding energy, the work function of a sample can be determined by bombarding it with a monochromatic X-ray source or UV source, and measuring the kinetic energy distribution of the electrons emitted.[51]

Photoelectron spectroscopy is done in a high-vacuum environment, since the electrons would be scattered by gas molecules if they were present. The light source can be a laser, a discharge tube, or a synchrotron radiation source.[52]

The concentric hemispherical analyser (CHA) is a typical electron energy analyzer, and uses an electric field to change the directions of incident electrons, depending on their kinetic energies. For every element and core (atomic orbital) there will be a different binding energy. The many electrons created from each of these combinations will show up as spikes in the analyzer output, and these can be used to determine the elemental composition of the sample.

Spacecraft

The photoelectric effect will cause spacecraft exposed to sunlight to develop a positive charge. This can be a major problem, as other parts of the spacecraft in shadow develop a negative charge from nearby plasma, and the imbalance can discharge through delicate electrical components. The static charge created by the photoelectric effect is self-limiting, though, because a more highly charged object gives up its electrons less easily.[53]

Moon dust

Light from the sun hitting lunar dust causes it to become charged through the photoelectric effect. The charged dust then repels itself and lifts off the surface of the Moon by electrostatic levitation.[54][55] This manifests itself almost like an "atmosphere of dust", visible as a thin haze and blurring of distant features, and visible as a dim glow after the sun has set. This was first photographed by the Surveyor program probes in the 1960s. It is thought that the smallest particles are repelled up to kilometers high, and that the particles move in "fountains" as they charge and discharge.

Night vision devices

Photons hitting a thin film of alkali metal or semiconductor material such as gallium arsenide in an image intensifier tube cause the ejection of photoelectrons due to the photoelectric effect. These are accelerated by an electrostatic field where they strike a phosphor coated screen, converting the electrons back into photons. Intensification of the signal is achieved either through acceleration of the electrons or by increasing the number of electrons through secondary emissions, such as with a Micro-channel plate. Sometimes a combination of both methods is used. Additional kinetic energy is required to move an electron out of the conduction band and into the vacuum level. This is known as the electron affinity of the photocathode and is another barrier to photoemission other than the forbidden band, explained by the band gap model. Some materials such as Gallium Arsenide have an effective electron affinity that is below the level of the conduction band. In these materials, electrons that move to the conduction band are all of sufficient energy to be emitted from the material and as such, the film that absorbs photons can be quite thick. These materials are known as negative electron affinity materials.

Cross section

The photoelectric effect is one interaction mechanism between photons and atoms. It is one of 12 theoretically possible interactions.[56]

At the high photon energies comparable to the electron rest energy of 511 keV, Compton scattering, another process, may take place. Above twice this (1.022 MeV) pair production may take place.[57] Compton scattering and pair production are an example of two other competing mechanisms.

Indeed, even if the photoelectric effect is the favoured reaction for a particular single-photon bound-electron interaction, the result is also subject to statistical processes and is not guaranteed, albeit the photon has certainly disappeared and a bound electron has been excited (usually K or L shell electrons at nuclear (gamma ray) energies). The probability of the photoelectric effect occurring is measured by the cross section of interaction, σ. This has been found to be a function of the atomic number of the target atom and photon energy. A crude approximation, for photon energies above the highest atomic binding energy, is given by:[58]

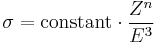
\sigma = \mathrm{constant} \cdot \frac{Z^n}{E^3}

Here Z is atomic number and n is a number which varies between 4 and 5. (At lower photon energies a characteristic structure with edges appears, K edge, L edges, M edges, etc.) The obvious interpretation follows that the photoelectric effect rapidly decreases in significance, in the gamma ray region of the spectrum, with increasing photon energy, and that photoelectric effect increases steeply with atomic number. The corollary is that high-Z materials make good gamma-ray shields, which is the principal reason that lead (Z = 82) is a preferred and ubiquitous gamma radiation shield.[59]

See also

Renewable energy portal

Electronics:

Physics:

People:

Lists:

References

  1. ^ a b Serway, Raymond A. (1990). Physics for Scientists & Engineers (3rd ed.). Saunders. p. 1150. ISBN 0030302587. http://books.google.com/?id=RUMBw3hR7aoC&q=inauthor:serway+photoelectric&dq=inauthor:serway+photoelectric. 
  2. ^ a b Sears, Francis W., Mark W. Zemansky and Hugh D. Young (1983), University Physics, Sixth Edition, Addison-Wesley, pp. 843–4. ISBN 0-201-07195-9.
  3. ^ Heinrich Hertz: Ueber den Einfluss des ultravioletten Lichtes auf die electrische Entladung. Annalen der Physik 267 (8), S. 983-1000, 1887.doi:10.1002/andp.18872670827
  4. ^ The American journal of science. (1880). New Haven: J.D. & E.S. Dana. p. 234
  5. ^ Weisstein, Eric W. (2007), "Eric Weisstein's World of Physics", Eric Weisstein's World of Science, Wolfram Research
  6. ^ a b Lenard, P. (1902). "Ueber die lichtelektrische Wirkung". Annalen der Physik 313 (5): 149–198. Bibcode 1902AnP...313..149L. doi:10.1002/andp.19023130510. 
  7. ^ a b Millikan, R. (1914). "A Direct Determination of "h."". Physical Review 4: 73–75. Bibcode 1914PhRv....4R..73M. doi:10.1103/PhysRev.4.73.2. 
  8. ^ Millikan, R. (1916). "A Direct Photoelectric Determination of Planck's "h"". Physical Review 7 (3): 355–388. Bibcode 1916PhRv....7..355M. doi:10.1103/PhysRev.7.355. http://www.fisica.net/quantica/millikan_a_direct_photoelectric_determination_of_plancks_h.pdf. 
  9. ^ Zhang, Q (1996). "Intensity dependence of the photoelectric effect induced by a circularly polarized laser beam". Physics Letters A 216: 125. Bibcode 1996PhLA..216..125Z. doi:10.1016/0375-9601(96)00259-9. 
  10. ^ Bubb, Frank (1924). "Direction of Ejection of Photo-Electrons by Polarized X-rays". Physical Review 23 (2): 137–143. Bibcode 1924PhRv...23..137B. doi:10.1103/PhysRev.23.137. 
  11. ^ Fromhold, A.T. (1991). Quantum mechanics for applied physics and engineering. Courier Dover Publications. pp. 5–6. ISBN 0486667413, 9780486667416. http://books.google.com/?id=3SOwc6npkIwC&pg=PA5&lpg=PA5. 
  12. ^ Ronald Gautreau, William Savin, Modern physics,McGraw-Hill Professional, 1999 ISBN 0070248303, pages 60–61
  13. ^ Stefan Hüfner (2003). Photoelectron Spectroscopy: Principles and Applications. Springer. ISBN 3540418024. 
  14. ^ a b c d e f g Report of the Board of Regents By Smithsonian Institution. Board of Regents, United States National Museum, Smithsonian Institution. p. 239.
  15. ^ G. C. Schmidt, Wied. Ann. Uiv. p. 708, 1898.
  16. ^ O. Knoblauch, Zeit.J. Physikalisclte Chemie, xxix. p. 527, 1899.
  17. ^ Petrova-Koch, V. (2009) "Milestones of Solar Conversion and Photovoltaics", High-Efficient Low-Cost Photovoltaics. Springer Series in Optical Sciences, Vol. 140. Berlin/Heidelberg: Springer. doi:10.1007/978-3-540-79359-5_1, ISBN 978-3-540-79358-8.
  18. ^ Smith, W., (1873) "Effect of Light on Selenium during the passage of an Electric Current". Nature, 1873-02-20, p.303.
  19. ^ Asimov, Asimov's Biographical Encyclopedia of Science and Technology 2nd Revised edition
  20. ^ Elster and Geitel arrange the metals in the following order with respect to their power of discharging negative electricity: rubidium, potassium, alloy of potassium and sodium, sodium, lithium, magnesium, thallium and zinc. For copper, platinum, lead, iron, cadmium, carbon, and mercury the effects with ordinary light are too small to be measurable. The order of the metals for this effect is the same as in Volta's series for contact-electricity, the most electropositive metals giving the largest photo-electric effect.
  21. ^ Hertz, Wied. Ann. xxxi. p. 983, 1887.
  22. ^ Hallwachs, Wied. Ann. xxxiii. p. 301, 1888.
  23. ^ Hoor, Repertorium des Physik, xxv. p. 91, 1889.
  24. ^ Bighi, C. R. cvi. p. 1349; cvii. p. 559, 1888
  25. ^ Stoletow. C. R. cvi. pp. 1149, 1593; cvii. p. 91; cviii. p. 1241; PhysikalUche Revue, Bd. i., 1892.
  26. ^ A. Stoletow (1888). "Sur une sorte de courants electriques provoques par les rayons ultraviolets". Comptes Rendus CVI: 1149.  (Reprinted in Phil. Mag. 26, 317, 1888; abstract in Beibl. Ann. d. Phys. 12, 605, 1888).
  27. ^ A. Stoletow (1888). "Sur les courants actino-electriqies au travers deTair". Comptes Rendus CVI: 1593.  (Abstract in Beibl. Ann. d. Phys. 12, 723, 1888).
  28. ^ A. Stoletow (1888). "Suite des recherches actino-electriques". Comptes Rendus CVII: 91.  (Abstract in Beibl. Ann. d. Phys. 12, 723, 1888).
  29. ^ A. Stoletow (1889). Comptes Rendus CVIII: 1241. 
  30. ^ A. Stoletow (1889). (in Russian)Journal of the Russian Physico-chemical Society 21: 159. 
  31. ^ A. Stoletow (1890). Journal de Physique 9: 468. 
  32. ^ Elster and Geitel, Wied. Ann. xxxviii. pp. 40, 497, 1889; xli. p. 161, 1890; xlii. p. 564, 1891; xliii. p. 225, 1892; lii. p. 433, 1894 ; lv. p. 684, 1895.
  33. ^ J. J. Thomson (March 2005). Conduction of Electricity Through Gases. Watchmaker Publishing. ISBN 9781929148493. http://books.google.com/books?id=x7KsD1GmIK0C. Retrieved 9 July 2011. 
  34. ^ Hallwachs, W. (1907). "Über die lichtelektrische Ermüdung". Annalen der Physik 328 (8): 459–516. Bibcode 1907AnP...328..459H. doi:10.1002/andp.19073280807. 
  35. ^ The International year book. (1900). New York: Dodd, Mead & Company. p. 659.
  36. ^ Bloch, Radium, p. 240, 1908
  37. ^ Thomson, Proc. Cambr., vol. 14, p. 417, 1907
  38. ^ Palmer, Frederic (1908). "Ionisation of Air by Ultra-violet Light". Nature 77 (2008): 582–582. Bibcode 1908Natur..77..582P. doi:10.1038/077582b0. 
  39. ^ Palmer, Frederic (1911). "Volume Ionization Produced by Light of Extremely Short Wave-Length". Physical Review (Series I) 32: 1–22. Bibcode 1911PhRvI..32....1P. doi:10.1103/PhysRevSeriesI.32.1. 
  40. ^ The Nobel Prize in Physics 1921
  41. ^ Lamb, Willis E.; Scully, Marlan O. (1968). "The photoelectric effect without photons". http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19680009569_1968009569.pdf. 
  42. ^ "The Nobel Prize in Physics 1921". Nobel Foundation. http://nobelprize.org/nobel_prizes/physics/laureates/1921/index.html. Retrieved 2008-10-09. 
  43. ^ Planck, Max (1901). "Ueber das Gesetz der Energieverteilung im Normalspectrum (On the Law of Distribution of Energy in the Normal Spectrum)". Annalen der Physik 4 (3): 553. Bibcode 1901AnP...309..553P. doi:10.1002/andp.19013090310. 
  44. ^ Robert Resnick, Basic Concepts in Relativity and Early Quantum Theory, Wiley, 1972, p. 137
  45. ^ a b Randall D. Knight, Physics for Scientists and Engineers With Modern Physics: A Strategic Approach, Pearson-Addison-Wesley, 2004, p. 1224
  46. ^ Roger Penrose, The Road to Reality: A Complete Guide to the Laws of the Universe, Knopf, 2005, p. 502 ISBN 0679454438
  47. ^ Robert Resnick, Basic Concepts in Relativity and Early Quantum Theory, Wiley, 1972, p. 138
  48. ^ J. Gethyn Timothy, ISSI Scientific Report 009, 2010, pp. 365–408, ISBN 9789292219383
  49. ^ R. W. Burns Television: an international history of the formative years, IET, 1998, ISBN 0852969147 p. 358
  50. ^ K. A. Tsokos, Cambridge Physics for the IB Diploma, Cambridge University Press, 2010 ISBN 0521138213 pp. 359–360
  51. ^ Stefan Hüfner Photoelectron Spectroscopy Principles and Applications. Springer, 3rd edition, 2003 ISBN 3540418024.
  52. ^ Weaver, J. H.; Margaritondo, G. (1979). "Solid-State Photoelectron Spectroscopy with Synchrotron Radiation". Science 206 (4415): 151–156. Bibcode 1979Sci...206..151W. doi:10.1126/science.206.4415.151. PMID 17801770. 
  53. ^ "Spacecraft charging". http://holbert.faculty.asu.edu/eee460/spacecharge.html. 
  54. ^ Bell, Trudy E., "Moon fountains", FirstScience.com, 2001-01-06.
  55. ^ Dust gets a charge in a vacuum
  56. ^ Evans, R. D. (1955). The Atomic Nucleus. Malabar, Fla.: Krieger. p. 673. ISBN 0898744148. http://www.archive.org/details/atomicnucleus032805mbp. 
  57. ^ Evans, R. D. (1955). The Atomic Nucleus. Malabar, Fla.: Krieger. p. 712. ISBN 0898744148. http://www.archive.org/details/atomicnucleus032805mbp. 
  58. ^ Davisson, C. M. (1965). Interaction of gamma-radiation with matter. pp. 37–78. http://adsabs.harvard.edu/abs/1965abgs.conf...37D. 
  59. ^ Knoll, Glenn F. (1999). Radiation Detection and Measurement. New York: Wiley. p. 49. ISBN 047149545X. http://sitemaker.umich.edu/gknoll/home. 

External links

Applets

Fundamental concepts
Primary energy sources
Fossil fuel (Coal, Petroleum, Natural gas) · Mineral fuel (Natural uranium) · Solar · Wind · Bioenergy (Biomass) · Water (Hydroenergy, Marine energy) · Geothermal
Energy carriers
Energy systems